P-Splines for GAMLSS

Description

Estimation of P-splines using an efficient local maximum likelihood approach to automatically select the smoothing parameter. According to the inventors of P-splines, pb stands for "penalized beta" splines or "Paul and Brian".

Usage

pb(x, k = 20, ...)

Arguments

x	The variable that should be used for estimation.
k	The dimension of the B-spline basis to represent the smooth term.
…	Further arguments passed to function s.

Details

Function pb() is an internal wrapper function that calls s to set up a smooth specification object that can be used for model fitting with gamlss2. Using pb(), an efficient local maximum likelihood approach is used to estimate the smoothing parameter. See the reference for details.

Value

The function returns a smooth specification object of class “ps.smooth.spec”, see also smooth.construct.ps.smooth.spec.

References

Eilers PHC, Marx BD (1996). “Flexible Smoothing with B-Splines and Penalties.” Statistical Science, 11(2), 89–121. doi:10.1214/ss/1038425655

Rigby RA, Stasinopoulos DM (2014). “Automatic Smoothing Parameter Selection in GAMLSS with an Application to Centile Estimation.” Statistical Methods in Medical Research, 23(4), 318–332. doi:10.1177/0962280212473302

See Also

gamlss2, smooth.construct.ps.smooth.spec

Examples

library("gamlss2")


## load head circumference data
data("dbhh", package = "gamlss.data")

## specify the model Formula
f <- head ~ pb(age) | pb(age) | pb(age) | pb(age)

## estimate model
b <- gamlss2(f, data = dbhh, family = BCT)

GAMLSS-RS iteration  1: Global Deviance = 26379.1782 eps = 0.390130     
GAMLSS-RS iteration  2: Global Deviance = 26205.4924 eps = 0.006584     
GAMLSS-RS iteration  3: Global Deviance = 26202.6475 eps = 0.000108     
GAMLSS-RS iteration  4: Global Deviance = 26202.2604 eps = 0.000014     
GAMLSS-RS iteration  5: Global Deviance = 26202.1179 eps = 0.000005     

## visualize estimated effects
plot(b, which = "effects")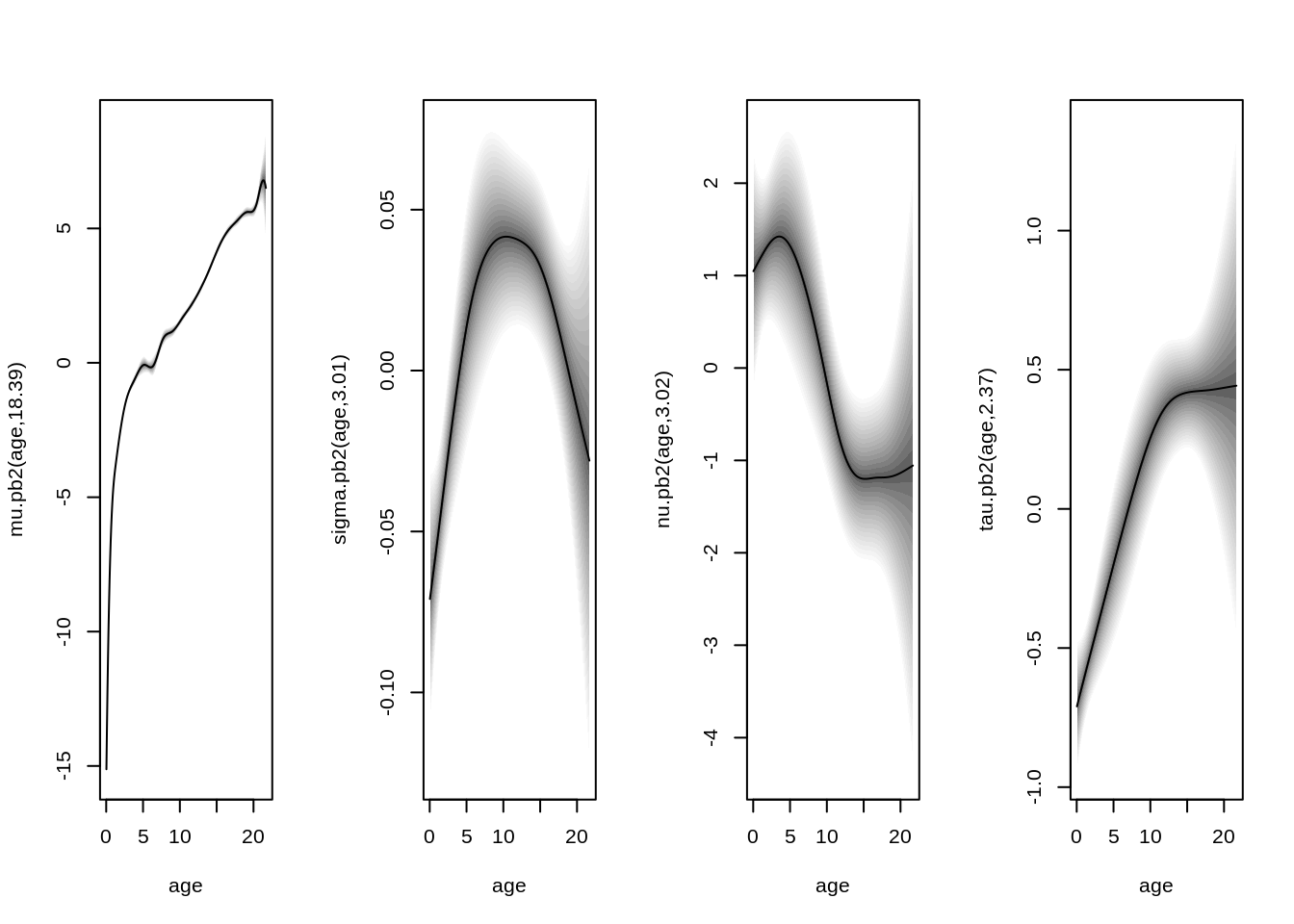

## plot diagnostics
plot(b, which = "resid")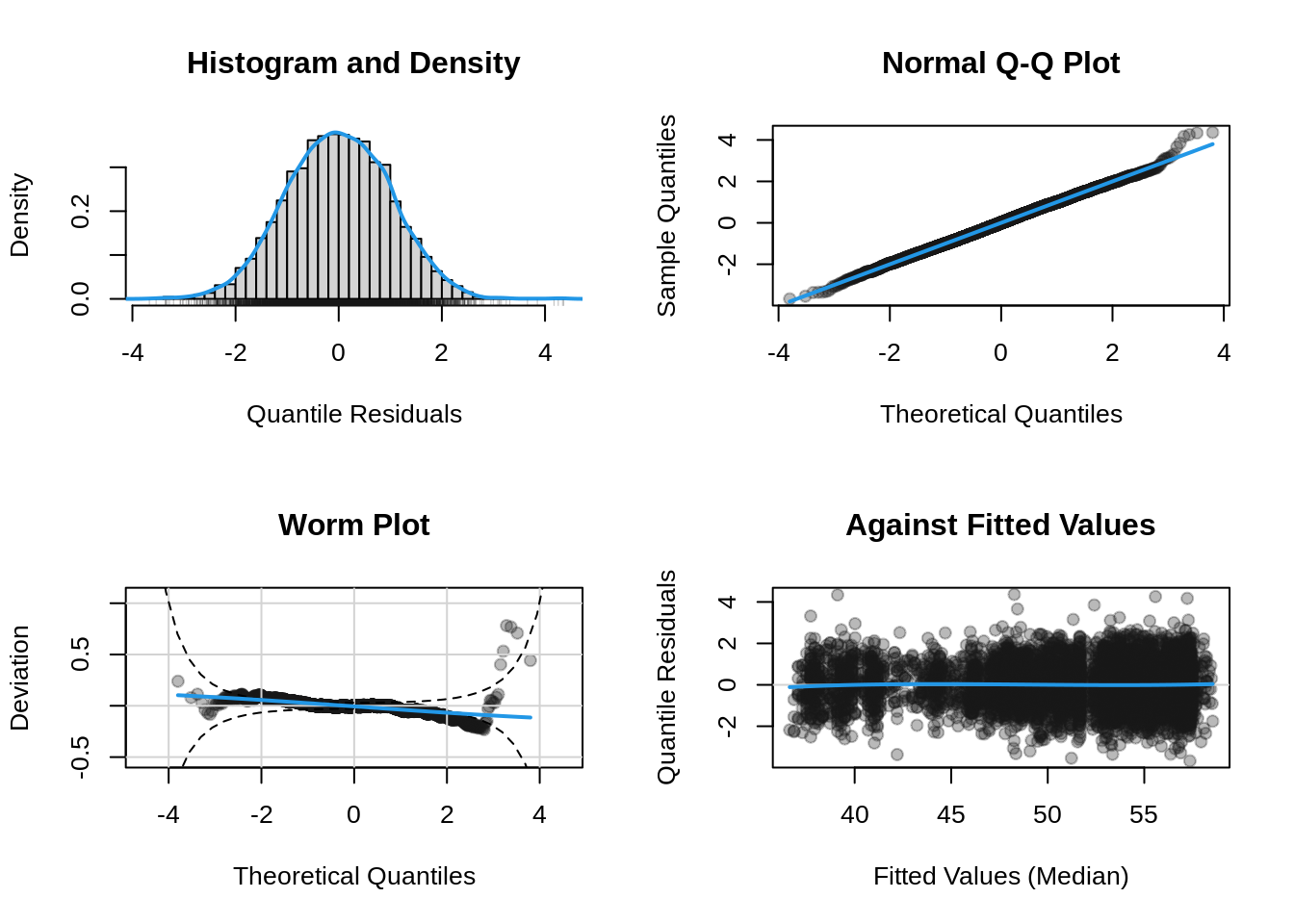

## predict quantiles
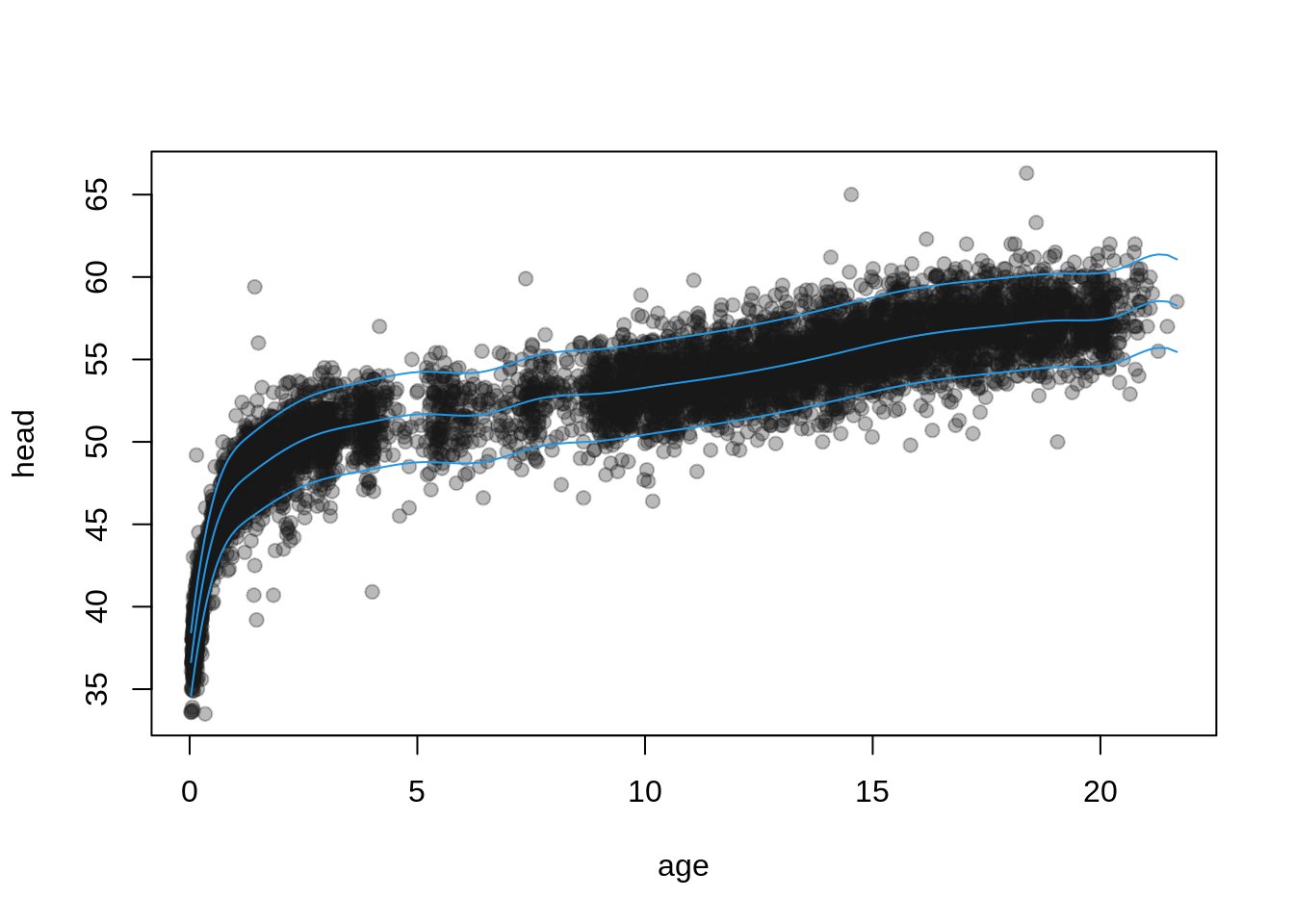
pq <- quantile(b, probs = c(0.05, 0.5, 0.95))

## plot
plot(head ~ age, data = dbhh, pch = 19,
  col = rgb(0.1, 0.1, 0.1, alpha = 0.3))
matplot(dbhh$age, pq, type = "l",
  lty = 1, col = 4, add = TRUE)