gamlss2

Extracting Fitted or Predicted Probability Distributions from gamlss2 Models

Description

Methods for gamlss2 model objects for extracting fitted (in-sample) or predicted (out-of-sample) probability distributions as distributions3 objects.

Usage

## S3 method for class 'gamlss2'
prodist(object, ...)

Arguments

object A model object of class gamlss2.

… Arguments passed on to predict.gamlss2, e.g., newdata.

Details

To facilitate making probabilistic forecasts based on gamlss2 model objects, the prodist method extracts fitted or predicted probability distribution objects. Internally, the predict.gamlss2 method is used first to obtain the distribution parameters (mu, sigma, tau, nu, or a subset thereof). Subsequently, the corresponding distribution object is set up using the GAMLSS class from the gamlss.dist package, enabling the workflow provided by the distributions3 package (see Zeileis et al. 2022).

Note that these probability distributions only reflect the random variation in the dependent variable based on the model employed (and its associated distributional assumption for the dependent variable). This does not capture the uncertainty in the parameter estimates.

Value

An object of class GAMLSS inheriting from distribution.

References

Zeileis A, Lang MN, Hayes A (2022). “distributions3: From Basic Probability to Probabilistic Regression.” Presented at useR! 2022 - The R User Conference. Slides, video, vignette, code at https://www.zeileis.org/news/user2022/.

Examples

library("gamlss2")


## packages, code, and data
library("distributions3")
data("cars", package = "datasets")

## fit heteroscedastic normal GAMLSS model
## stopping distance (ft) explained by speed (mph)
m <- gamlss2(dist ~ s(speed) | s(speed), data = cars, family = NO)

GAMLSS-RS iteration  1: Global Deviance = 405.737 eps = 0.128969     
GAMLSS-RS iteration  2: Global Deviance = 405.7368 eps = 0.000000

## obtain predicted distributions for three levels of speed
d <- prodist(m, newdata = data.frame(speed = c(10, 20, 30)))
print(d)

                                  1                                   2 
"GDF NO(mu = 23.06, sigma = 10.06)" "GDF NO(mu = 58.98, sigma = 18.53)" 
                                  3 
"GDF NO(mu = 96.14, sigma = 34.12)"

## obtain quantiles (works the same for any distribution object 'd' !)
quantile(d, 0.5)

       1        2        3 
23.05774 58.98303 96.14450

quantile(d, c(0.05, 0.5, 0.95), elementwise = FALSE)

     q_0.05    q_0.5    q_0.95
1  6.509283 23.05774  39.60620
2 28.505214 58.98303  89.46086
3 40.028584 96.14450 152.26042

quantile(d, c(0.05, 0.5, 0.95), elementwise = TRUE)

         1          2          3 
  6.509283  58.983035 152.260421

## visualization
plot(dist ~ speed, data = cars)
nd <- data.frame(speed = 0:240/4)
nd$dist <- prodist(m, newdata = nd)
nd$fit <- quantile(nd$dist, c(0.05, 0.5, 0.95))
matplot(nd$speed, nd$fit, type = "l", lty = 1, col = "slategray", add = TRUE)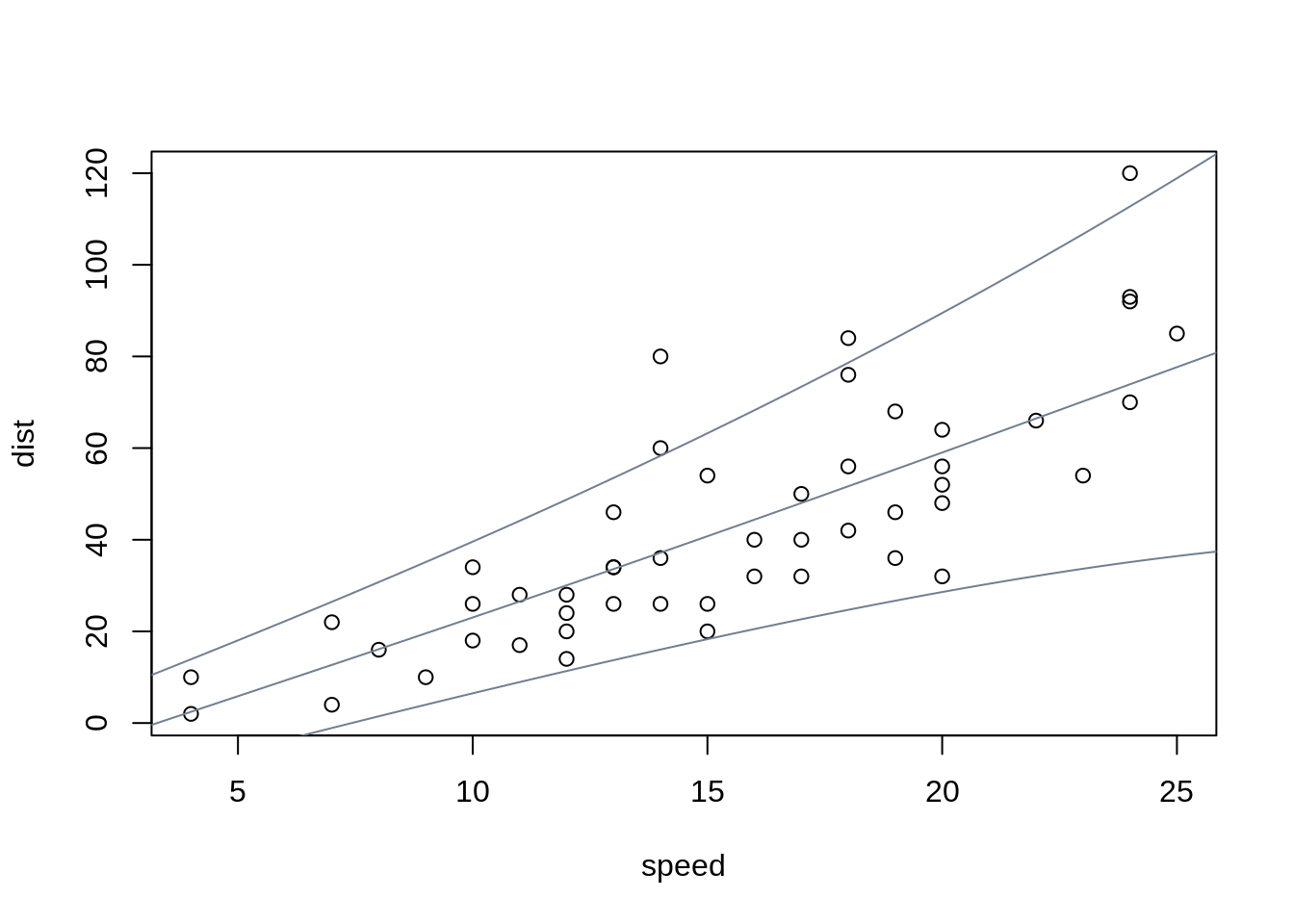

## moments
mean(d)

       1        2        3 
23.05774 58.98303 96.14450

variance(d)

        1         2         3 
 101.2187  343.3312 1163.9053

## simulate random numbers
random(d, 5)

       r_1      r_2      r_3       r_4       r_5
1 12.92953 41.32227 26.13464  17.97513  36.90059
2 60.26480 58.82597 57.91182  77.34323  53.19475
3 74.14045 41.67091 49.83402 108.81556 145.99628

## density and distribution
pdf(d, 50 * -2:2)

        d_-100        d_-50          d_0        d_50        d_100
1 1.291599e-34 1.405182e-13 0.0028687701 0.001099050 7.901284e-15
2 2.223063e-18 6.622130e-10 0.0001357331 0.019143272 1.857756e-03
3 7.765882e-10 1.211145e-06 0.0002204765 0.004684784 1.161925e-02

cdf(d, 50 * -2:2)

        p_-100        p_-50          p_0       p_50     p_100
1 1.055415e-34 1.911829e-13 0.0109571049 0.99629637 1.0000000
2 4.738088e-18 2.030474e-09 0.0007281644 0.31390760 0.9865732
3 4.479859e-09 9.188654e-06 0.0024149871 0.08809582 0.5449892

## Poisson example
data("FIFA2018", package = "distributions3")
m2 <- gamlss2(goals ~ s(difference), data = FIFA2018, family = PO)

GAMLSS-RS iteration  1: Global Deviance = 355.3922 eps = 0.045332     
GAMLSS-RS iteration  2: Global Deviance = 355.3922 eps = 0.000000

d2 <- prodist(m2, newdata = data.frame(difference = 0))
print(d2)

                   1 
"GDF PO(mu = 1.237)"

quantile(d2, c(0.05, 0.5, 0.95))

[1] 0 1 3

## note that log_pdf() can replicate logLik() value
sum(log_pdf(prodist(m2), FIFA2018$goals))

[1] -177.6961

logLik(m2)

'log Lik.' -177.6961 (df=2.005144)